ГДЗ Страница 132 Математика 4 класс 2 часть белый учебник, Дорофеев, Миракова, Бука

ОТВЕТЫ К ЗАДАНИЯМ

6. Вычисли значения выражений.
712 * 306 + 158314 : 26;
28 * (80067 − 53296) + 6302;
290268 : 36 + 514 * 407;
(90705 − 48 * 160) : 25 + 4986;
800 * 100 − 32490 : 57 + 10486 : 98;
4428 : 123 − (32 * 816 − 26000) : 14;
(8032 − 595) : 37 * 50 − 10000 : 40;
(20655 : 85 + 757) * (6370 : 182 − 29).

Решение по действиям

Запись в строку

712 * 306 + 158314 : 26 = 217872 + 6089 = 223961

28 * (80067 − 53296) + 6302 = 28 * 26771 + 6302 = 74958 + 6302 = 755890

290268 : 36 + 514 * 407 = 8063 + 209198 = 217261

(90705 − 48 * 160) : 25 + 4986 = (90705 − 7680) : 25 + 4986 = 83025 : 25 + 4986 = 3321 + 4986 = 8307

800 * 100 − 32490 : 57 + 10486 : 98 = 80000 − 570 + 107 = 79430 + 107 = 79537

4428 : 123 − (32 * 816 − 26000) : 14 = 36 − (26112 − 26000) : 14 = 36 − 112 : 14 = 36 − 8 = 28

(8032 − 595) : 37 * 50 − 10000 : 40 = 7437 : 37 * 50 − 250 = 201 * 50 − 250 = 10050 − 250 = 9800

(20655 : 85 + 757) * (6370 : 182 − 29) = (243 + 757) * (35 − 29) = 1000 * 6 = 6000

Ответы к теме «Геометрия»

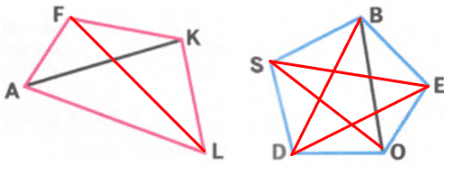
1. В каждом многоугольнике на чертеже проведено по одной диагонали. Запиши обозначения этих диагоналей. Запиши обозначения диагоналей, которые еще можно провести.

Решение

Многоугольник AFKL:
проведенные диагонали: AK;
не проведенные диагонали: FL.

Многоугольник SBEOD:
проведенные диагонали: BO;
не проведенные диагонали: SE, SO, BD, DE.

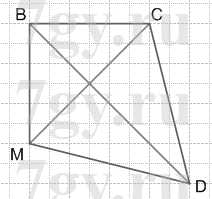
2. В четырехугольнике MBCD проведена диагональ MC. Какую еще диагональ можно провести в этом четырехугольнике? Сколько всего диагоналей можно провести в четырехугольнике?

Решение

В четырехугольнике еще можно провести диагональ BD. Всего в четырехугольнике может быть 2 диагонали.

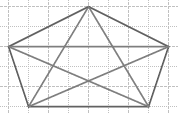
3. Сколько диагоналей можно провести в пятиугольнике? Выполни чертеж. Какую фигуру образуют эти диагонали?

Решение

В пятиугольнике можно провести пять диагоналей.
Диагонали образуют фигуру − звезду.

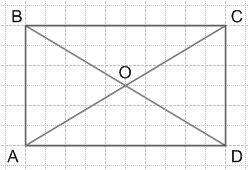
4. Как называется четырехугольник, диагонали которого равны и точкой пересечения делится пополам?

Решение

Четырехугольник, диагонали которого равны и точкой пересечения делится пополам называется прямоугольником.

5. Какие свойства диагоналей прямоугольника ты знаешь?

Решение

Свойства диагоналей прямоугольника:
1) Диагонали прямоугольника имеют одинаковую длину.
2) Каждая диагональ прямоугольника делит прямоугольник на два одинаковых прямоугольных треугольника.
3) Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам.
4) Точка пересечения диагоналей называется центром прямоугольника.

6. Попробуй определить на глаз, какой из данных углов на чертеже является острым; прямым; тупым. Проверь свою догадку с помощью чертежного угольника.

Решение