ГДЗ Страница 96 учебник по математике 4 класс 2 часть Моро
ОТВЕТЫ К ЗАДАНИЯМ
Повтори всё, что ты знаешь о геометрических фигурах (с. 125-126).
1. Назови знакомые тебе геометрические фигуры, начерти их в тетради и обозначь буквами.
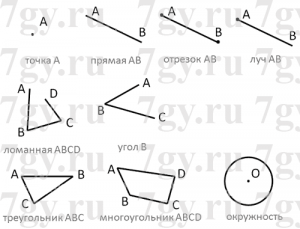
2. Что ты знаешь о многоугольниках? Сколько вершин, углов и сторон у двенадцатиугольника?
Многоугольники по числу углов. Если в многоугольнике 3 угла — это треугольник, если 4 — это четырехугольник, если 5 — пятиугольник.
В любом многоугольнике число углов равно числу сторон и вершин.
В двенадцатиугольнике 12 углов, 12 вершин и 12 сторон.
3. Какие виды треугольников ты знаешь? Может ли прямоугольный треугольник быть равносторонним? разносторонним? Может ли тупоугольный треугольник быть равнобедренным? Начерти в тетради равнобедренный прямоугольный треугольник.
Треугольники, от вида углов, бывают остроугольные, тупоугольные и прямоугольные. В зависимости от длин сторон треугольники бывают разносторонними, равносторонними, равнобедренными.
Прямоугольный треугольник не может быть равносторонним, но может быть разносторонним или равнобедренным.
Тупоугольный треугольник может быть равнобедренным.
4. Какие виды четырёхугольников ты знаешь? Продолжи предложения:
1) Прямоугольник — это такой четырёхугольник, у которого … .
2) Квадрат — это такой прямоугольник, у которого … .
Прямоугольник, квадрат.
1) Прямоугольник — это четырехугольник, у которого все углы прямые.
2) Квадрат — это прямоугольник, у которого все стороны равны.
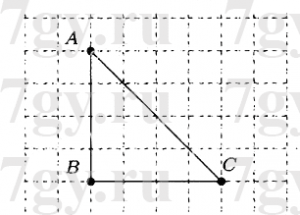
5. 1) Среди четырёхугольников, изображённых на рисунке 1, найди прямоугольники и запиши их названия; подчеркни название квадрата.
2) Найди периметр прямоугольника ОРКС и площадь квадрата. Объясни, почему четырёхугольник ABCD нельзя назвать квадратом.
1) ОРКС, FKEM, EKМD.
2) Периметр прямоугольника ОРКС равен 15 • 2 + 9 • 2 = 48 (мм)
Площадь квадрата KMEF равна 9 • 9 = 81 ( м2). Четырехугольник ABCD нельзя назвать квадратом, так как он не прямоугольник.
6. Определи вид каждого треугольника, если его периметр находят так:
1) 3 + 4 + 5=12 (см);
2) 3 • 2 + 4=10 (см);
3) 5 • 3=15 (см).
1) разносторонний треугольник;
2) равнобедренный треугольник;
3) равносторонний треугольник.
7. Рассмотри рисунок 2 на полях и запиши названия всех прямоугольных, остроугольных и тупоугольных треугольников; подчеркни названия равнобедренных треугольников.
Прямоугольные треугольники: ABO, ВСК, ВОК, CDO.
Остроугольные треугольники: AOD.
Тупоугольные треугольники: АКО, CDK, СОК.
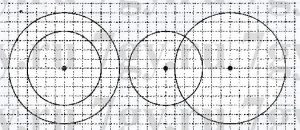
8. Начерти 2 окружности с радиусами 2 см и 3 см сначала с общим центром, а потом с разными центрами.
9. Найди длину ломаной АОКС (рис. 2).
Длина ломанной АОКС равна 30 + 32 + 39 = 101 мм